from config import *
from config import make_df_ECB
%matplotlib inlineLa legge di Okun
Introduzione
All’inizio degli anni ’60, la crescita economica e la riduzione della disoccupazione erano temi centrali per gli economisti americani. Arthur M. Okun si specializzò nello studio del prodotto potenziale, ovvero il livello di output raggiungibile in condizioni di disoccupazione ottimale (all’epoca stimata intorno al 4%) e di una domanda sufficiente ad assorbire l’offerta disponibile.
Dal punto di vista pratico, era fondamentale quantificare l’impatto di una variazione della disoccupazione sulla produzione. Ad esempio, una riduzione del tasso di disoccupazione dal 6% al 4,5% avrebbe avvicinato il prodotto al suo livello potenziale, riducendo il “gap” tra output effettivo e potenziale. Al contrario, un aumento della disoccupazione avrebbe avuto l’effetto opposto.
L’obiettivo di Okun era individuare una relazione quantitativa tra il prodotto nazionale lordo (PNL) e il tasso di disoccupazione. In questa sezione analizzeremo le due metodologie con cui Okun ha stimato tale relazione.
I. Differenze percentuali
In questo primo esercizio, viene utilizzato un modello di regressione lineare con intercetta, dove le variazioni nel tasso di disoccupazione Y vengono regredite sulle variazioni percentuali di PNL X. Tutti i dati sono rilevati trimestralmente. Le serie utilizzate sono: - https://fred.stlouisfed.org/series/UNRATE per il tasso di disoccupazione - https://www.nber.org/research/data/american-business-cycle-continuity-and-change-historic-data-tables per il PNL
# Carica il dataset contenente il tasso di disoccupazione da un file CSV
unemp = pd.read_csv('UNRATE_OKUN.csv')
# Converte la colonna delle date in formato datetime per una gestione più efficace delle serie temporali
unemp['observation_date'] = pd.to_datetime(unemp['observation_date'], format='%Y-%m-%d')
# Imposta la colonna delle date come indice del DataFrame per lavorare con serie temporali
unemp = unemp.set_index('observation_date')
# Raggruppa i dati per trimestre calcolando la media del tasso di disoccupazione per ogni periodo
unemp = unemp.groupby(pd.Grouper(freq='Q'))['UNRATE'].mean().to_frame()
# Converte l'indice in un PeriodIndex con frequenza trimestrale per una gestione più accurata delle serie storiche
unemp.index = pd.PeriodIndex(unemp.index, freq='Q')
# Calcola la variazione trimestrale del tasso di disoccupazione
unemp['change_unemp'] = unemp['UNRATE'].diff()
# Rimuove eventuali valori NaN generati dalla differenziazione
unemp = unemp.dropna()
# Filtra i dati fino al quarto trimestre del 1960 per allinearsi al periodo di interesse
unemp = unemp[unemp.index <= '1960Q4']
# Visualizza le prime righe del DataFrame risultante
unemp.head()| UNRATE | change_unemp | |
|---|---|---|
| observation_date | ||
| 1948Q2 | 3.666667 | -0.066667 |
| 1948Q3 | 3.766667 | 0.100000 |
| 1948Q4 | 3.833333 | 0.066667 |
| 1949Q1 | 4.666667 | 0.833333 |
| 1949Q2 | 5.866667 | 1.200000 |
# Carica il dataset contenente il prodotto nazionale lordo (PNL) da un file CSV
gnp = pd.read_csv('abcq.csv')
# Crea una nuova colonna per la data, combinando l'anno e il trimestre
gnp['observation_date'] = gnp['year'].astype(str) + 'Q' + gnp['quarter'].astype(str)
# Imposta la colonna 'observation_date' come indice del DataFrame
gnp = gnp.set_index('observation_date')
# Converte l'indice in un PeriodIndex con frequenza trimestrale per una gestione più accurata delle serie storiche
gnp.index = pd.PeriodIndex(gnp.index, freq='Q')
# Seleziona solo la colonna 'GNP' e la converte in un DataFrame
gnp = gnp['GNP'].to_frame()
# Calcola la variazione percentuale trimestrale del prodotto nazionale lordo
gnp['pct_change_gnp'] = gnp['GNP'].pct_change() * 100
# Rimuove eventuali valori NaN generati dalla differenziazione
gnp = gnp.dropna()
# Filtra i dati per mantenere solo il periodo tra il secondo trimestre del 1948 e il quarto trimestre del 1960
gnp = gnp[(gnp.index <= '1960Q4') & (gnp.index >= '1948Q2')]
# Visualizza le prime righe del DataFrame risultante
gnp.head()| GNP | pct_change_gnp | |
|---|---|---|
| observation_date | ||
| 1948Q2 | 257.5 | 3.000000 |
| 1948Q3 | 264.5 | 2.718447 |
| 1948Q4 | 265.9 | 0.529301 |
| 1949Q1 | 260.5 | -2.030839 |
| 1949Q2 | 257.0 | -1.343570 |
# Unisce i DataFrame 'unemp' e 'gnp' utilizzando l'indice come chiave di unione
df = pd.merge(unemp, gnp, right_index=True, left_index=True)
# Definisce la variabile indipendente X (le variazioni percentuali del PNL)
X = df['pct_change_gnp']
# Definisce la variabile dipendente Y (le variazioni del tasso di disoccupazione)
Y = df['change_unemp']
# Aggiunge un termine costante al modello di regressione per tener conto dell'intercetta
X = sm.add_constant(X)
# Crea il modello di regressione lineare (OLS) con Y come dipendente e X come indipendente
model = sm.OLS(Y, X)
# Adatta il modello ai dati
results = model.fit()
# Stampa i risultati della regressione
print(results.summary()) OLS Regression Results
==============================================================================
Dep. Variable: change_unemp R-squared: 0.631
Model: OLS Adj. R-squared: 0.623
Method: Least Squares F-statistic: 83.74
Date: Fri, 21 Mar 2025 Prob (F-statistic): 3.51e-12
Time: 18:54:20 Log-Likelihood: -19.032
No. Observations: 51 AIC: 42.06
Df Residuals: 49 BIC: 45.93
Df Model: 1
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
const 0.4238 0.065 6.546 0.000 0.294 0.554
pct_change_gnp -0.2669 0.029 -9.151 0.000 -0.325 -0.208
==============================================================================
Omnibus: 6.492 Durbin-Watson: 1.585
Prob(Omnibus): 0.039 Jarque-Bera (JB): 5.400
Skew: 0.713 Prob(JB): 0.0672
Kurtosis: 3.714 Cond. No. 3.12
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.L’interpretazione dei coefficienti è immediata: tenendo fisso il PNL il tasso di disoccupazione aumenterà di .42 punti da un trimestre all’altro, in quanto la crescita della forza lavoro e i processi tecnologici spingeranno in basso il rapporto occupati/forza lavoro attiva. Per ogni aumento di 1 punto percentuale del PNL, il tasso di disoccupazione diminuirà di .27 punti. Di converso, un aumento del tasso di disoccupazione di 1 punto percentuale comporterà una riduzione del PNL del 3.7%.
Si può notare che i valori ottenuti non sono dissimili da quelli dell’articolo originale, che riporta una approssimazione: \[
Y = .3 - .3X
\] In questi casi, il metodo di rilevazione dei dati ed eventuali manipolazioni successive possono essere responsabili di leggere variazioni nei coefficienti.
# Calcola le previsioni per la variazione del tasso di disoccupazione usando il modello di regressione
df['pred_unemp_change'] = results.predict(X)
# Ordina i dati in base alla variazione percentuale del PNL (X)
sorted_data = df.sort_values(by='pct_change_gnp')
# Crea una figura con un solo subplot
fig, ax = plt.subplots(1, 1)
# Aggiunge una linea orizzontale a y=0 per facilitare la lettura del grafico
ax.axhline(y=0, color='silver', linewidth=2)
# Crea un grafico a dispersione per visualizzare le osservazioni reali (variabile dipendente vs variabile indipendente)
ax.scatter(df['pct_change_gnp'], df['change_unemp'], alpha=0.7, label="Osservazioni", color=bmh_colors[0])
# Aggiunge la linea di regressione (legge di Okun) sul grafico
ax.plot(sorted_data['pct_change_gnp'], sorted_data['pred_unemp_change'],
color=bmh_colors[1], label="Legge Di Okun")
# Imposta il titolo del grafico e lo allinea a sinistra
ax.set_title(f"US, 1948-1960", loc='left')
# Imposta le etichette degli assi
ax.set_xlabel('Variazione Del PNL')
ax.set_ylabel('Variazione Del Tasso Di Disoccupazione')
# Aggiunge la griglia al grafico per facilitare la lettura
ax.grid(True)
# Aggiunge la legenda al grafico
ax.legend()
# Ottimizza il layout del grafico per una visualizzazione migliore
plt.tight_layout()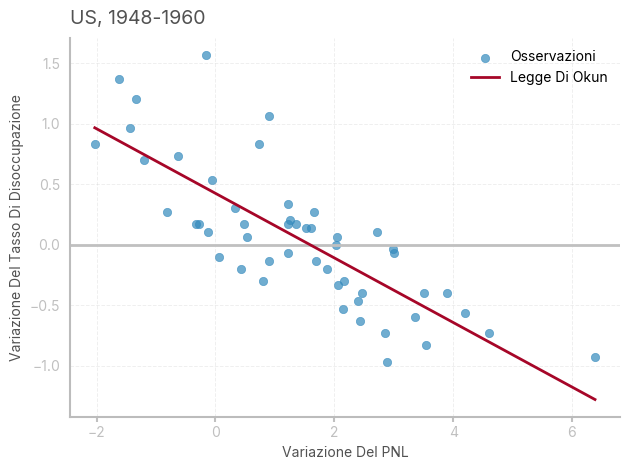
II. Elasticità
Questo metodo è molto importante dal punto di vista pratico, in quanto consente di associare dei coefficienti ai livelli di PNL e tasso di occupazione, piuttosto che alle loro variazioni percentuali. Questo servirà in seguito per stimare il PNL potenziale. In particolare, si ipotizza che:
ci sia elesticità costante (\(a\)) fra il rapporto tra prodotto osservato (\(A\)-actual) e potenziale (\(P\)) ed il rapporto fra tasso di occupazione (\(N\)) e tasso di occupazione potenziale (\(N_F\)). In simboli: \(\frac{N}{N_F} = \left( \frac{A}{P} \right)^a\)
il prodotto potenziale cresca ad un tasso costante \(r\) in funzione del tempo: \(P-t = P_0 e^{rt}\)
Il risultato restituisce l’equazione del modello, i cui parametri verranno stimati tramite OLS: \[\ln N_t = \ln \frac{N_F}{P_0^a} + a \ln A_t - (ar)t\]
# Calcola il tasso di occupazione sottraendo il tasso di disoccupazione da 100
df['emprate'] = 100 - df['UNRATE']
# Calcola il logaritmo naturale del tasso di occupazione
df['logN'] = np.log(df['emprate'])
# Calcola il logaritmo naturale del Prodotto Nazionale Lordo (PNL)
df['logA'] = np.log(df['GNP'])
# Crea una variabile trend che va da 1 fino al numero di osservazioni (usata per catturare l'effetto di trend nel modello)
df['trend'] = range(1, 1+len(df))
# Mostra le prime righe del DataFrame risultante per una rapida verifica
df.head()| UNRATE | change_unemp | GNP | pct_change_gnp | pred_unemp_change | emprate | logN | logA | trend | |
|---|---|---|---|---|---|---|---|---|---|
| observation_date | |||||||||
| 1948Q2 | 3.666667 | -0.066667 | 257.5 | 3.000000 | -0.376806 | 96.333333 | 4.567814 | 5.551020 | 1 |
| 1948Q3 | 3.766667 | 0.100000 | 264.5 | 2.718447 | -0.301666 | 96.233333 | 4.566776 | 5.577841 | 2 |
| 1948Q4 | 3.833333 | 0.066667 | 265.9 | 0.529301 | 0.282564 | 96.166667 | 4.566083 | 5.583120 | 3 |
| 1949Q1 | 4.666667 | 0.833333 | 260.5 | -2.030839 | 0.965804 | 95.333333 | 4.557380 | 5.562603 | 4 |
| 1949Q2 | 5.866667 | 1.200000 | 257.0 | -1.343570 | 0.782388 | 94.133333 | 4.544712 | 5.549076 | 5 |
# Definisce la variabile dipendente Y (logaritmo naturale del tasso di occupazione)
Y = df['logN']
# Definisce la matrice delle variabili indipendenti X (logaritmo del PNL e trend)
X = df[['logA', 'trend']]
# Aggiunge una costante a X per includere l'intercetta nel modello
X = sm.add_constant(X)
# Crea un modello di regressione lineare ordinario (OLS) con Y come variabile dipendente e X come variabili indipendenti
model = sm.OLS(Y,X)
# Calcola i risultati del modello
results = model.fit()
# Stampa il sommario dei risultati della regressione
print(results.summary()) OLS Regression Results
==============================================================================
Dep. Variable: logN R-squared: 0.854
Model: OLS Adj. R-squared: 0.848
Method: Least Squares F-statistic: 140.6
Date: Fri, 21 Mar 2025 Prob (F-statistic): 8.53e-21
Time: 18:54:21 Log-Likelihood: 196.88
No. Observations: 51 AIC: -387.8
Df Residuals: 48 BIC: -382.0
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 2.9807 0.101 29.463 0.000 2.777 3.184
logA 0.2853 0.018 15.662 0.000 0.249 0.322
trend -0.0043 0.000 -16.516 0.000 -0.005 -0.004
==============================================================================
Omnibus: 3.874 Durbin-Watson: 0.521
Prob(Omnibus): 0.144 Jarque-Bera (JB): 3.453
Skew: -0.636 Prob(JB): 0.178
Kurtosis: 2.930 Cond. No. 4.24e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 4.24e+03. This might indicate that there are
strong multicollinearity or other numerical problems.Dove il coefficiente di logA è l’elasticità dell’output al tasso di occupazione; il coefficiente del tempo è, per definizione, il prodotto tra il coefficiente di logA e il tasso di crescita costante del prodotto potenziale; l’intercetta restituisce il benchmark \(P_0\) per ogni livello di \(N_F\), che verrà preso pari a 96.
Iterate regressioni hanno portato Okun al seguente risultato: \[
P = A \left( 1+ .032 \left( U-4 \right) \right)
\]
from mpl_toolkits.mplot3d import Axes3D
# Crea una nuova figura per il grafico 3D con dimensioni personalizzate
fig = plt.figure(figsize=(10, 7))
# Aggiunge un subplot 3D alla figura
ax = fig.add_subplot(111, projection='3d')
# Crea un grafico scatter 3D con logA, trend e logN, etichettato come 'Osservazioni'
ax.scatter(df['logA'], df['trend'], df['logN'], label='Osservazioni', alpha=0.7)
# Definisce i valori di intervallo per logA e trend (in modo da poter creare una superficie)
logA_range = np.linspace(df['logA'].min(), df['logA'].max(), 20)
trend_range = np.linspace(df['trend'].min(), df['trend'].max(), 20)
# Crea una griglia di valori per logA e trend
logA_grid, trend_grid = np.meshgrid(logA_range, trend_range)
# Calcola i valori adattati della superficie utilizzando i parametri stimati dal modello di regressione
fitted_values = results.params['const'] + results.params['logA'] * logA_grid + results.params['trend'] * trend_grid
# Aggiunge la superficie al grafico 3D, colorandola con un colore specifico e un'alpha di trasparenza
ax.plot_surface(logA_grid, trend_grid, fitted_values, color=bmh_colors[1], alpha=0.5)
# Imposta le etichette degli assi
ax.set_xlabel('logA')
ax.set_ylabel('Trend')
ax.set_zlabel('logN')
# Imposta il titolo del grafico
ax.set_title('Legge Di Okun, livelli')
# Modifica l'angolazione della visualizzazione per rendere più chiara la superficie
ax.view_init(elev=20, azim=45)
# Aggiunge la legenda al grafico
plt.legend()
# Mostra il grafico
plt.show()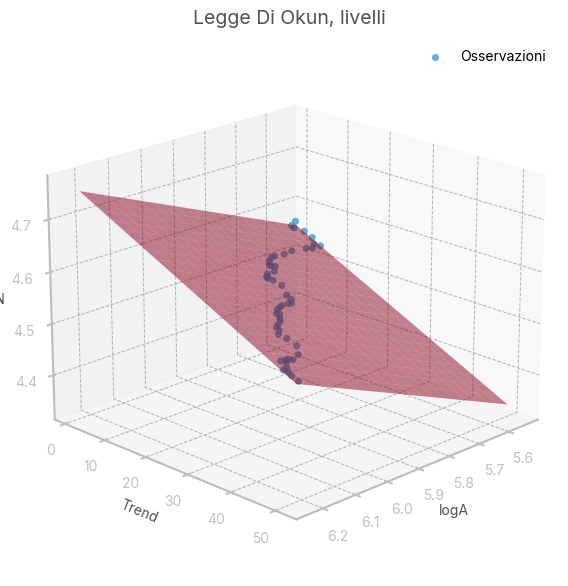
# Calcola il PNL potenziale utilizzando la formula di Okun (assumendo un tasso di disoccupazione ottimale del 4%)
df['potential_gnp'] = df['GNP']*(1+.032*(df['UNRATE']-4))
# Crea un grafico con un subplot
fig, ax = plt.subplots(1,1)
# Filtra i dati dal primo trimestre del 1954 e traccia il PNL osservato
df[df.index>='1954Q1']['GNP'].plot(label='PNL', ax=ax)
# Filtra i dati dal primo trimestre del 1954 e traccia il PNL potenziale calcolato
df[df.index>='1954Q1']['potential_gnp'].plot(label='PNL potenziale', ax=ax)
# Aggiunge etichette agli assi
plt.ylabel('PNL (in miliardi di dollari)')
plt.xlabel('Trimestre')
# Aggiunge il titolo al grafico, posizionandolo a sinistra
plt.title('Calcolo Del PNL Potenziale Secondo Okun', loc='left')
# Mostra la legenda per distinguere le due linee
plt.legend()
# Regola la disposizione del layout per ottimizzare lo spazio
plt.tight_layout()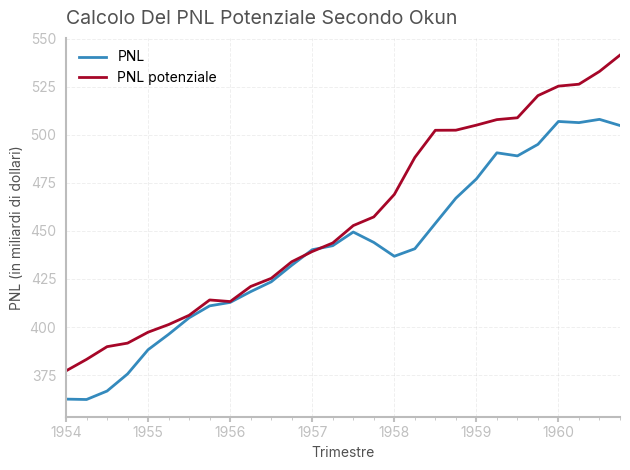
E oggi?
# Funzione per estrarre i dati dal datawarehouse della BCE
def make_df_ECB(key, obs_name):
"""Estrae i dati dal datawarehouse della BCE"""
url_ = 'https://sdw-wsrest.ecb.europa.eu/service/data/' # URL di base per il servizio web della BCE
format_ = '?format=csvdata' # Impostazione del formato dei dati in CSV
df = pd.read_csv(url_+key+format_) # Legge i dati CSV dal servizio web BCE usando la chiave
df = df[['TIME_PERIOD', 'OBS_VALUE']] # Seleziona le colonne di interesse (periodo e valore osservato)
df['TIME_PERIOD'] = pd.to_datetime(df['TIME_PERIOD']) # Converte il periodo in formato datetime
df = df.set_index('TIME_PERIOD') # Imposta il periodo come indice del dataframe
df.columns = [obs_name] # Rinomina la colonna con il nome della variabile
return df
# Chiave per il tasso di disoccupazione
unemp_rate_key = 'LFSI/Q.I9.S.UNEHRT.TOTAL0.15_74.T' # Codice identificativo del tasso di disoccupazione
unemp = make_df_ECB(unemp_rate_key, 'unemp') # Ottieni i dati dal database ECB
unemp['change_unemp'] = unemp['unemp'].diff() # Calcola la variazione del tasso di disoccupazione
# Chiave per il PIL (GDP)
gdp_key = 'MNA/Q.Y.I9.W2.S1.S1.B.B1GQ._Z._Z._Z.EUR.LR.N' # Codice identificativo del PIL
gdp = make_df_ECB(gdp_key, 'gdp') # Ottieni i dati dal database ECB
gdp['pct_change_gdp'] = gdp['gdp'].pct_change()*100 # Calcola la variazione percentuale del PIL
# Unisci i dati del tasso di disoccupazione e del PIL
df = pd.merge(unemp, gdp, right_index=True, left_index=True)
df = df.dropna() # Rimuove le righe con valori NaN
# Mostra le prime righe del dataframe risultante
df.head()| unemp | change_unemp | gdp | pct_change_gdp | |
|---|---|---|---|---|
| TIME_PERIOD | ||||
| 2000-04-01 | 9.128157 | -0.223128 | 2.433026e+06 | 0.896372 |
| 2000-07-01 | 8.982247 | -0.145910 | 2.449339e+06 | 0.670484 |
| 2000-10-01 | 8.751499 | -0.230748 | 2.460466e+06 | 0.454298 |
| 2001-01-01 | 8.532471 | -0.219028 | 2.487753e+06 | 1.109010 |
| 2001-04-01 | 8.472304 | -0.060167 | 2.489155e+06 | 0.056341 |
# Definizione delle variabili indipendente (X) e dipendente (Y)
X = df['pct_change_gdp'] # Variabile indipendente: variazione percentuale del PIL
Y = df['change_unemp'] # Variabile dipendente: variazione del tasso di disoccupazione
# Aggiunta dell'intercetta (costante) al modello
X = sm.add_constant(X) # Aggiunge una colonna di 1 alla variabile indipendente per includere l'intercetta
# Creazione del modello di regressione lineare (OLS)
model = sm.OLS(Y, X) # OLS: Ordinary Least Squares (minimi quadrati ordinari)
# Fitting del modello (stima dei parametri)
results = model.fit() # Calcola i risultati del modello di regressione
# Stampa del sommario dei risultati
print(results.summary()) # Visualizza un riepilogo completo dei risultati della regressione OLS Regression Results
==============================================================================
Dep. Variable: change_unemp R-squared: 0.006
Model: OLS Adj. R-squared: -0.005
Method: Least Squares F-statistic: 0.5490
Date: Fri, 21 Mar 2025 Prob (F-statistic): 0.460
Time: 18:54:22 Log-Likelihood: 2.0828
No. Observations: 99 AIC: -0.1656
Df Residuals: 97 BIC: 5.025
Df Model: 1
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
const -0.0286 0.024 -1.170 0.245 -0.077 0.020
pct_change_gdp -0.0101 0.014 -0.741 0.460 -0.037 0.017
==============================================================================
Omnibus: 42.392 Durbin-Watson: 0.743
Prob(Omnibus): 0.000 Jarque-Bera (JB): 109.819
Skew: 1.560 Prob(JB): 1.42e-24
Kurtosis: 7.110 Cond. No. 1.84
==============================================================================
Notes:
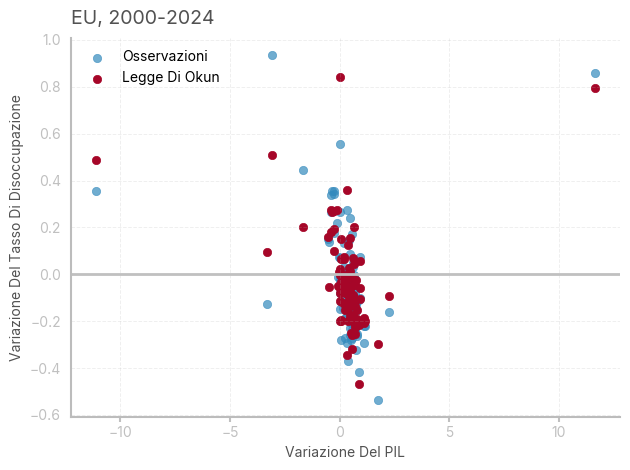
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Il modello non passa il test di zero-slopes, e nessun coefficiente è significativo. Il modello mostra autocorrelazione positiva (il limite inferiore di DW è intorno a 1.5). come si può constatare dal seguente grafico, la relazione tra variazione nel tasso di disoccupazione e variazione percentuale del PIL è molto debole in Europa, nel periodo considerato.
# Calcolo delle previsioni della variazione del tasso di disoccupazione
df['pred_unemp_change'] = results.predict(X)
# Ordinamento dei dati per la variabile indipendente (PIL)
sorted_data = df.sort_values(by='pct_change_gdp')
# Creazione della figura e dell'asse per il grafico
fig, ax = plt.subplots(1, 1)
# Aggiunta di una linea orizzontale a y=0
ax.axhline(y=0, color='silver', linewidth=2)
# Creazione del grafico a dispersione (scatter plot) per le osservazioni effettive
ax.scatter(df['pct_change_gdp'], df['change_unemp'], alpha=0.7, label="Osservazioni", color=bmh_colors[0])
# Aggiunta della retta di regressione (Legge di Okun)
ax.plot(sorted_data['pct_change_gdp'], sorted_data['pred_unemp_change'],
color=bmh_colors[1], label="Legge Di Okun")
# Titolo e etichette degli assi
ax.set_title(f"EU, 2000-2024", loc='left')
ax.set_xlabel('Variazione Del PIL')
ax.set_ylabel('Variazione Del Tasso Di Disoccupazione')
# Aggiunta di una griglia al grafico
ax.grid(True)
# Aggiunta della legenda
ax.legend()
# Ottimizzazione della disposizione del grafico
plt.tight_layout()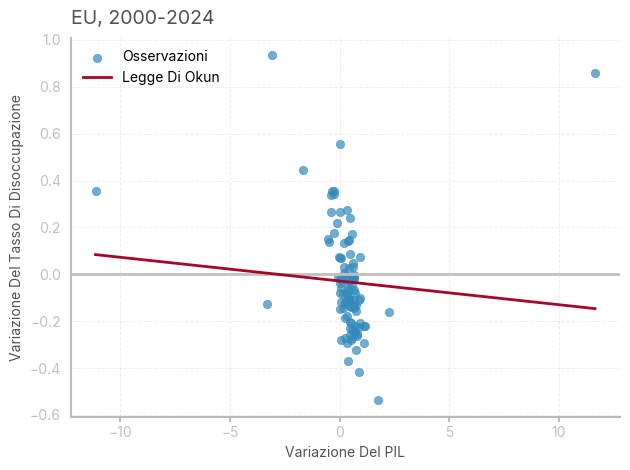
Come esercizio, ho replicato il modello aggiungendo i lag di GDP e disoccupazione (come suggerito dal test di DW) - il modello ora riporta un elevato \(R^2\) e coefficienti significativi, tuttavia ha perso il sapore caratteristico dell’originale curva di Okun.
# Creazione delle variabili laggate per la variazione del PIL e per la disoccupazione
df['pct_change_gdp_lag1'] = df['pct_change_gdp'].shift(1)
df['unemp_lag1'] = df['change_unemp'].shift(1)
# Rimozione dei valori nulli generati dalla creazione dei lag
df = df.dropna()
# Creazione delle variabili indipendenti (incluso il termine costante)
X = df[['pct_change_gdp', 'pct_change_gdp_lag1', 'unemp_lag1']]
X = sm.add_constant(X)
# Variabile dipendente (cambio del tasso di disoccupazione)
Y = df['change_unemp']
# Creazione del modello di regressione dinamica con stima robusta degli errori (HAC)
model_dyn = sm.OLS(Y, X).fit(cov_type='HAC', cov_kwds={'maxlags': 4})
# Visualizzazione dei risultati del modello
print(model_dyn.summary()) OLS Regression Results
==============================================================================
Dep. Variable: change_unemp R-squared: 0.760
Model: OLS Adj. R-squared: 0.752
Method: Least Squares F-statistic: 272.3
Date: Fri, 21 Mar 2025 Prob (F-statistic): 3.23e-46
Time: 18:54:22 Log-Likelihood: 71.457
No. Observations: 98 AIC: -134.9
Df Residuals: 94 BIC: -124.6
Df Model: 3
Covariance Type: HAC
=======================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------------
const 0.0219 0.015 1.476 0.140 -0.007 0.051
pct_change_gdp -0.0260 0.012 -2.166 0.030 -0.050 -0.002
pct_change_gdp_lag1 -0.0766 0.005 -16.759 0.000 -0.086 -0.068
unemp_lag1 0.6233 0.042 14.905 0.000 0.541 0.705
==============================================================================
Omnibus: 5.478 Durbin-Watson: 2.021
Prob(Omnibus): 0.065 Jarque-Bera (JB): 6.170
Skew: 0.289 Prob(JB): 0.0457
Kurtosis: 4.085 Cond. No. 8.21
==============================================================================
Notes:
[1] Standard Errors are heteroscedasticity and autocorrelation robust (HAC) using 4 lags and without small sample correction# Previsione dei cambiamenti nel tasso di disoccupazione usando il modello dinamico
df['pred_unemp_change_2'] = model_dyn.predict(X)
# Ordinamento dei dati in base alla variazione del PIL
sorted_data = df.sort_values(by='pct_change_gdp')
# Creazione del grafico
fig, ax = plt.subplots(1, 1)
# Aggiunta della linea orizzontale per il valore zero
ax.axhline(y=0, color='silver', linewidth=2)
# Creazione dello scatter plot per le osservazioni
ax.scatter(df['pct_change_gdp'], df['change_unemp'], alpha=0.7, label="Osservazioni", color=bmh_colors[0])
# Creazione della linea della Legge di Okun basata sulle previsioni
ax.scatter(sorted_data['pct_change_gdp'], sorted_data['pred_unemp_change_2'],
color=bmh_colors[1], label="Legge Di Okun")
# Titolo del grafico
ax.set_title(f"EU, 2000-2024", loc='left')
# Etichette degli assi
ax.set_xlabel('Variazione Del PIL')
ax.set_ylabel('Variazione Del Tasso Di Disoccupazione')
# Aggiunta della griglia
ax.grid(True)
# Aggiunta della legenda
ax.legend()
# Ottimizzazione del layout
plt.tight_layout()